Arximed aksiomu

Arximed aksiomu və ya Arximed prinsipi və ya Arximed mülkiyyəti — Qədim yunan riyaziyyatçısı Arximedin adını daşıyan riyazi ifadələr.

Seqmentlər üçün Arximed aksiomu

Bu təklif əvvəlcə Knidli Evdoks Kəmiyyətlər münasibətləri nəzəriyyəsində formalaşdırıldı (Evdoksun kəmiyyət anlayışı həm nömrələri, həm də davamlı kəmiyyətləri əhatə edir: parçalar, sahələr, həcmlər):

İki miqdar varsa $a$ və $b$, $a$ $b$-dən azdırsa, sonra $a$ komponent olaraq götürüb,kifayət qədər $b$-ni kənarlaşdıra bilərik:

$\underbrace {a+a+\ldots +a} _{n}>b$

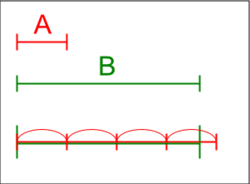
Məsələn, seqmentlər üçün Arximed aksiomu belə səslənir: əgər iki seqment verilirsə, onlardan daha kiçik olanı kifayət qədər dəfə təxirə salmaqla daha böyük hissəni örtə bilər.

Arximed aksiomu ifadəsi mənasız görünür,lakin əsl mənası sonsuz və ya sonsuz böyük miqdarda olmamasıdır. Beləliklə, bu aksiom qeyri-standart analizdə yerinə yetirilmir: hiperreal ədədlər dəstində sonsuz və sonsuz böyük miqdarlar var. Bu cür elementlər Arximedin aksiomunu qane edə bilməz. Digər nümunələr mümkündür.

Arximed əmlakının razı olduğu riyazi quruluşlar,arximediya adlanır,məsələn, Arximed sahəsi və Arximed qrupu və yerinə yetirilməyənlər isə - arximediya deyil.

Tarixi

Riyaziyyatda Arximedin aksiomu kimi tanınan aksiom, əslində ilk olaraq Knidli Evdoks tərəfindən tərtib edilmişdir. Bu təklif əslində əsl ədədlərin ilk aksiomatik nəzəriyyəsi olan münasibətlər nəzəriyyəsində əsas rol oynadı. Buna görə də buna Evdoksun aksiomu da deyilir.

Evdoksun nəzəriyyəsi bizə Evklidin təqdimatında gəldi.("Başlanğıclar", Kitab V).

Kəmiyyətlərin bir-biri ilə əlaqəli olduğu deyilir,əgər onlar çoxaldılarsa onlar bir-birini üstələyə bilərlər. "Başlanğıclar",V Kitab,4-cü tərif

Evdoksun aksiomu - Arximed, Evdoks tərəfindən icad edilən "tükənmə metodu" adını daşıyır -Rieman inteqralıvə Darb nəzəriyyəsi analoqundan istifadə etməklə rəqəmlərin sahələrini, bədən həcmlərini, qövslərin uzunluqlarını tapmaq üsuludur. Bununla birlikdə, Arximed bu sahədə ən böyük nəticələrə nail oldu. Öz metodundan istifadə edərək Evdoks sahələrin və həcmlərin hesablanmasına dair bir neçə teoremi ciddi şəkildə sübut etdi. Üstəlik, Qədim Yunanıstanda ardıcıllıq anlayışı olmadığından, ardıcıllığın həddi olduğu üçün Arximed hər konkret tapşırıqda arqumenti yenidən təkrarlamalı idi. Beləliklə, Arximed öz yazılarında Evdoksun - Arximedin aksiomlarını tərtib etmiş və istifadə etmişdir. Eyni zamanda, Arximed özü The Quadrature of the Parabolakitabının giriş hissəsində bu aksiomun sələfləri tərəfindən istifadə edildiyini və Evdoksun əsərlərində əhəmiyyətli rol oynadığını vurğulayır..

Müasir tərif

Xətti sifarişli qrup

Qoy $G$ — xətti sifarişli qrup,$a$ və $b$ — $G$-in müsbət elementləri olsun. $a$ elementi $b$ elementinə münasibətdə sonsuz kiçikdir,lakin əgər hər hansı bir təbii $n$ bərabərsizliyi varsa $b$ $a$-ya münasibətdəsonsuz böyükdür:

$\underbrace {a+a+\ldots +a} _{n}<b$

$G$ qrupu əgər Arximedin aksiomu yerinə yetirilirsə, Arximediya adlanır: $G$ -də $a$ elementləri cütü yoxdur,belə ki, $b$ $a$$b$ - $b$-yə münasibətdə sonsuz kiçikdir.

Sifarişli sahə

Qoy $K$ — sifarişli bir sahə olsun. Hər sifariş edilmiş sahə xətti sifariş edilmiş bir qrup olduğundan, onda sonsuz kiçik və sonsuz böyük elementlərin yuxarıdakı bütün tərifləri, həmçinin Arximed aksiomunun tərtib edilməsi qüvvədə qalır. Bununla birlikdə, bir sıra spesifik xüsusiyyətlər mövcuddur, buna görə də Arximed aksiomunun formalaşdırılması sadələşdirilmişdir.

Qoy $a,b$ $K$-nın müsbət elementləri olsun.

• $a$ elementi $b$ elementinə nisbətində sonsuz kiçikdir,yalnız onda $a/b$ $1\in K$ -yə münasibətdə sonsuz kiçik olur (belə elementlər sadəcə sonsuz kiçik adlanır).
• $a$ elementi $b$ elementinə nisbətən sonsuz dərəcədə böyükdür, yalnız onda $a/b$ $1\in K$-yə münasibətdə sonsuz böyük olur (belə elementlər sadəcə sonsuz böyük adlanır).

Sonsuz kiçik və sonsuz böyük elementlər sonsuz elementlər adı altında birləşdirilir.

Müvafiq olaraq, Arximed aksiomunun tərtib edilməsi sadələşdirilir: sifariş edilmiş sahə $K$ sonsuz kiçik elementlərə sahib deyilsə və ya eyni dərəcədə sonsuz böyük elementlərə sahib deyilsə Arximed mülkiyyətinə malikdir. Sonsuz kiçik (və ya sonsuz böyük) bir elementin tərifini burada genişləndirsək, Arximed aksiomunun aşağıdakı formulasını alırıq:

Hər hansı $a$ elementi, $K$ sahəsi üçün təbii $n$ $n>a$ kimi elementləri mövcuddur.

Və ya, ekvivalent formula:

Sahənin hər hansı bir müsbət $\varepsilon >0$ elementi üçün təbii $n$ $1/n<\varepsilon$ kimi elementləri mövcuddur.

Nümunələr və əks misallar

Həqiqi ədədlər toplusu

Arximed sahəsinin ən məşhur nümunəsi həqiqi ədədlər toplusudur. Həqiqi ədədlər toplusunu rasional dəstin tamamlanması hesab etsək (məsələn, Dedekind kəsiyindən istifadə etməklə),onda həqiqi ədədlər üçün Arximed əmlakı rasional ədədlərin ona sahib olmasıdır.Bununla əlaqədar olaraq qeyd etmək lazımdır ki, David Hilbert tərəfindən təklif olunan həqiqi ədədlərin aksiomu sistemlərindən birində (Hilbertin aksiomatikası),həqiqi ədədlər toplusu, maksimum arximediya sifariş edilmiş sahə, yəni Arximed aksiomunu təmin edən sifarişli bir sahə olaraq təyin olunaraq (yəni sonsuz elementləri ehtiva etmir),daha böyük bir Arximediya sifariş edilmiş sahəyə genişləndirilə bilməz.

Arximed olmayan sifarişli sahə

Arximed aksiomunun yerinə yetirilmədiyi sifariş edilmiş bir sahənin nümunəsi (daha doğrusu, əks misal) olaraq, real əmsallar, yəni forma funksiyaları ilə rasional funksiyalar toplusunu nəzərdən keçiririk

$R(x)={\frac {a_{n}x^{n}+\ldots +a_{1}x+a_{0}}{b_{m}x^{m}+\ldots +b_{1}x+b_{0}}}$

Ümumi əlavə və vurma əməliyyatlarına gəlincə bu məcmu bir sahə meydana gətirir. Rasional funksiyaların cəminə sifarişin əlaqəsini aşağıdakı kimi təqdim edirik.$f$ və $g$ — iki rasional funksiyadır. Deyirik ki,$f>g$ əgər bəzi məhəllələrdə $+\infty$ ilə fərq olduqda $f-g$ ciddi bir müsbət işarəyə malik olur.Bu şərt,rasional funksiyaların əmsalları$f$ və $g$ baxımından tərtib edilə bilər. Fərqi $f-g$ çoxbucaqlı + müntəzəm rasional fraksiya şəklində yazırıq:

$f(x)-g(x)=c_{n-m}x^{n-m}+\ldots +c_{1}x+c_{0}+{\frac {d_{k}x^{k}+\ldots +d_{1}x+d_{0}}{x^{m}+b_{m-1}x^{m-1}+\ldots +b_{1}x+b_{0}}}$

burada sağ tərəfdəki son müddət müntəzəm rasional fraksiyadır, yəni ədədi dərəcəsi məxrəc dərəcəsindən azdır: $k<m$.Biz də məxrəcin ən yüksək əmsalı $b_{m}$ $1$ olduğunu hesab edəcəyik. Sonra $f>g$ olarsa yalnız onda hər hansı $c_{n-m}>0$,ya çoxbucaqlı hissə itir və ya $d_{k}>0$ olur.Təqdim olunan qaydanın düzgünlüyünü yoxlamaq asandır (tətbiq olunan əlaqənin həqiqətən sifariş əlaqəsi olduğunu və bu əlaqənin sahə əməliyyatlarına uyğun olduğunu təsdiqləmək lazımdır).

Beləliklə, rasional funksiyaların cəmi sifarişli bir sahə təşkil edir. Qeyd edək ki, bu həqiqi ədədlər sahəsinin uzantısıdır, lakin Arximedin aksiomu burada tətbiq edilmir(əvvəlki hissənin sonuna baxın!).Həqiqətən, $1$ və $x$ elementlərini nəzərdən keçirək. Aydındır ki, $n$ natural sayı nə olursa olsun, bərabərsizliyi saxlayır:

$\underbrace {1+1+\ldots +1} _{n}=n\cdot 1<x$

Başqa sözlə, $x$ birinə münasibətdə sonsuz böyük bir sahə elementidir. Beləliklə, bu sahədə Arximedin aksiomu tutmur.

Həmçinin bax

• Arximed
• Arximed qanunu
• Arximed spiralı

Ədəbiyyat

• История математики. 1. М.: «Наука». Под ред. А. П. Юшкевича. 2003.
• Евклид. Начала. 1. М.—Л.: Главное Издательство Технико-Теоретической Литературы. Перевод Д. Д. Мордухай—Болтовского. 1948.
• Гильберт, Д. Основания геометрии. М.—Л.: Главное Издательство Технико-Теоретической Литературы. 1948.
• Бурбаки, Н. Очерки по истории математики. М.: Издательство иностранной литературы. Пер. И. Г. Башмаковой под ред. К. А. Рыбникова. 1963.

• Archimède : fizika tarixi (isp.)
• Riyazi Analiz fənninin proqramı

Portal:Elm	Portal:Fizika
Portal:Elm	Portal:Fizika