Menelay teoremi

Menelay teoremi, transversal haqqında teorem və ya tam dördtərəfli haqqında teorem — Afin həndəsəsinin klassik teoremidir.

Bu, İskəndəriyyəli Menelaya aid edilən planimetriya teoremidir.

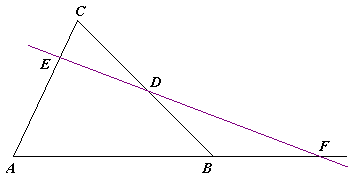
Əgər ${\displaystyle A',B'}$ və ${\displaystyle C'}$ nöqtələri uyğun olaraq ${\displaystyle \triangle ABC}$ üçbucağının ${\displaystyle BC,CA}$ və ${\displaystyle AB}$ tərəfləri yaxud onların uzantıları üzərində olarlarsa, onda onlar yalnız və yalnız o zaman kollinear^[1] olarlar ki,

${\displaystyle {\frac {AB'}{B'C}}\cdot {\frac {CA'}{A'B}}\cdot {\frac {BC'}{C'A}}=-1.}$

burada ${\displaystyle {\frac {AB'}{B'C}}}$, ${\displaystyle {\frac {CA'}{A'B}}}$ və ${\displaystyle {\frac {BC'}{C'A}}}$ istiqamətlənmiş düz xətt parçalarının nisbətidir.