Loqarifm

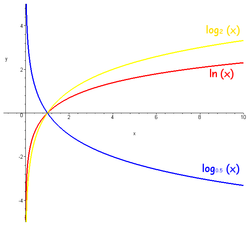
Loqarifm - b ədədini almaq üçün a əsasını yüksəltmək lazım gələn qüvvət üstünə b ədədinin a əsasına görə loqarifmi deyilir: $\log _{a}b\,$ . "Loqarifm" terminini elmə ilk dəfə şotlandiya alimi Con Nepyer (1550-1617) gətirmişdir.

Loqarifmik eyniliklər

Aşağıdakı cədvəlin 1-ci tərəfində düstur, 2-ci tərəfində isə bu düsturlara aid misallar verilmişdir:

	Düstur	Misal
Vurma	$\log _{b}(xy)=\log _{b}(x)+\log _{b}(y)\,$	$\log _{3}(243)=\log _{3}(9\cdot 27)=\log _{3}(9)+\log _{3}(27)=2+3=5\,$
Bölmə	$\log _{b}\!\left({\frac {x}{y}}\right)=\log _{b}(x)-\log _{b}(y)\,$	$\log _{2}(16)=\log _{2}\!\left({\frac {64}{4}}\right)=\log _{2}(64)-\log _{2}(4)=6-2=4$
Yüksəltmə	$\log _{b}(x^{p})=p\log _{b}(x)\,$	$\log _{2}(64)=\log _{2}(2^{6})=6\log _{2}(2)=6\,$
Kökaltı ifadə	$\log _{b}{\sqrt[{p}]{x}}={\frac {\log _{b}(x)}{p}}\,$	$\log _{10}{\sqrt {1000}}={\frac {1}{2}}\log _{10}1000={\frac {3}{2}}=1.5$

Colin Byfleet, Educational video on logarithms, İstifadə tarixi: 12/10/2010
Edward Wright, Translation of Napier's work on logarithms, 2007-06-27 tarixində orijinalından arxivləşdirilib, İstifadə tarixi: 12/10/2010