Üçbucaq
Üçbucaq — müstəvinin bir düz xətt üzərində olmayan 3 nöqtəsini cüt-cüt və ardıcıl şəkildə birləşdirən 3 düz xətt parçasından ibarət fiqur. Nöqtələr onun təpələri, parçalar onun tərəfləridir.
Üçbucağın təpələri adətən böyük latın hərfləri ilə (A, B, C), uyğun təpədəki bucaqların dərəcə ölçüsü yunan hərfləri (α,β,γ) ilə, uyğun təpənin qarşısındakı tərəfin uzunluğu isə əlyazma latın hərfləri ilə (a, b, c) işarə olunur.
| Üçbucağın növləri | ||
|---|---|---|
 İtibucaqlı üçbucaq |
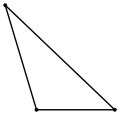 Korbucaqlı üçbucaq |
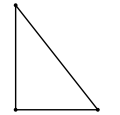 Düzbucaqlı üçbucaq |
 Müxtəliftərəfli üçbucaq |
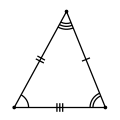
Bərabəryanlı üçbucaq | 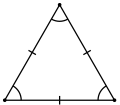 Bərabərtərəfli üçbucaq |
- Bütün bucaqları iti bucaq (90-dərəcədən kiçik) olan üçbucağa itibucaqlı üçbucaq deyilir.
- Bir bucağı düz bucaq (90°-yə bərabər) olan üçbucağa düzbucaqlı üçbucaq deyilir. Üçbucağın yalnız bir bucağı düz bucaq ola bilər. Düzbucaqlı üçbucağın qalan iki bucağı iti (90°-dən az) bucaqdır.
- Bir bucağı kor bucaq (90°-dən böyük) olan üçbucağa korbucaqlı üçbucaq deyilir. Üçbucağın yalnız bir bucağı kor bucaq ola bilər. Korbucaqlı üçbucağın qalan iki bucağı iti bucaqdır.
- İki tərəfi bərabər olan üçbucağa bərabəryanlı üçbucaq deyilir.
- Tərəflərinin üçü də bərabər olan üçbucağa bərabərtərəfli (yaxud düzgün üçbucaq) deyilir. Bucaqlarının üçü də 60°-ə bərabərdir.
Düzbucaq qarşısındakı tərəf hipotenuz, digər 2 tərəf isə katet adlanır.
30°-li bucaq qarşısındakı katet hipotenuzun yarısına, 60°-li bucaq qarşısında katet digər katetin kökdə 3 mislinə bərabərdir.
Düzbucaqlı üçbucağın xaricinə çəkilmiş çevrənin radiusu hipotenuzun yarısına bərabərdir. Hipetonuza çəkilmiş median hipetonuzun yarısına bərabərdir
Üçbucağın verilmiş təpəsini qarşı tərəfin ortası ilə birləşdirən parça üçbucağın medianı adlanır. Median üçbucağı sahələri bərabər olan 2 üçbucağa ayırır. Üçbucağın hər üç medianı bir nöqtədə kəsişir və kəsişmə nöqtəsində təpədən hesablanmaqla 2:1 nisbətində bölünür. Kəsişmə nöqtəsi üçbucağın ağırlıq mərkəzi adlanır. Hipetonuza çəkilmiş median hipetonuzun yarısına bərabərdir.
ma =
mb =
mc =
Üçbucağın verilmiş təpəsini qarşı tərəflə birləşdirən və təpədəki bucağı yarıya bölən parçaya üçbucağın tənböləni deyilir. Üçbucağın tənbölənləri bir nöqtədə kəsişir və həmin nöqtə daxilə çəkilmiş çevrənin mərkəzidir.
Teorem.
Üçbucağın tənböləni çəkildiyi tərəfi digər iki tərəflə mütənasib hissələrə bölür.
Üçbucağın təpəsindən qarşı tərəfə, yaxud onun uzantısına çəkilmiş perpendikulyar xətt, üçbucağın hündürlüyü adlanır. Üçbucağın üç hündürlüyü bir nöqtədə kəsişir.
Bərabəryanlı və bərabərtərəfli üçbucaqda oturacağa çəkilmiş hündürlük həm median, həm də tənböləndir.
Üçbucağın bütün tərəflərinə toxunan çevrəyə onun daxilinə çəkilmiş çevrə deyilir. Üçbucağın daxilinə çəkilmiş çevrə var və yeganədir. Üçbucağın hər üç təpəsindən keçən çevrəyə onun xaricinə Üçbucağın iki tərəfinin ortasını birləşdirən parçaya üçbucağın orta xətti deyilir. Orta xətt paralel olduğu tərəfin yarısına bərabərdir. Bərabəryanlı üçbucaqda oturacağa çəkilmiş hündürlük, median və tənbölən üst-üstə düşür. Bunu tərsi də doğrudur: Əgər tənbölən, hündürlük və median üst-üstə düşərsə, onda üçbucaq bərabəryanlıdır. Tərəfləri müxtəlif olan üçbucağın bir təpəsindən çəkilmiş tənbölən həmin təpədən çəkilmiş median və hündürlük arasında yerləşir. Üçbucağın tərəflərinin orta perpendikulyarları da bir nöqtədə kəsişir və həmin nöqtə xaricə çəkilmiş çevrənin mərkəzi ilə üst-üstə düşür.
- Üçbucağın daxili bucaqlarının cəmi 180°-dir: .
- Üçbucağın xarici bucaqlarının cəmi 360°-dir.
- Üçbucağın böyük bucaq qarşısındakı tərəfi kiçik bucaq qarşısındakı tərəfdən böyük olur.
- Üçbucağın hər hansı bir tərəfinin uzunluğu digər iki tərəfin uzunluqları cəmindən kiçik, fərqindən isə böyükdür (bu üçbucaq bərabərsizliyi adlanır):
- Üçbucağın tənbölənləri bir nöqtədə kəsişir.
- Üçbucağın medianları bir nöqtədə kəsişir.
üçbucağının sahəsi ilə işarə olunur.
- 1-ci düstur:
və ya
Üçbucağın sahəsi, tərəfinin uzunluğu ilə bu tərəfə çəkilmiş olan hündürlüyü hasilinin yarısına bərabərdir.
- 2-ci düstur (Heron düsturu):
(yarımperimetr) — Heron düsturu
- 3-cü düstur
-də tərəflər bu tərəflərin qarşısındakı bucaqlar isə uyğun olaraq α, β, γ olarsa,
1)
2)
- Əgər üçbucağı tərəfləri olmaqla bərabərtərəflidirsə, onda
- Əgər üçbucağının daxilinə çəkilmiş çevrənin radiusunu , xaricinə çəkilmiş çevrənin radiusunu , perimetrini isə ilə işarə etsək, onda
1)
2)
- Əgər üçbucağı düzbucaqlı üçbucaq, katetləri isə və -dirsə, onda
üçbucağının tərəflərini və , yarımperimetrini (), tərəfinə çəkilmiş medianını , tənbölənini , hündürlüyünü isə ilə işarə etsək, onda
və -ni 3-cü düsturda elə yerinə qoymaq lazımdır ki, kökaltı ifadə müsbət olsun.
- Riyaziyyat, qəbul imtahanlarına hazırlaşanlar, yuxarı sinif şagirdləri və müəllimlər üçün dərs vəsaiti, M. H. Yaqubov, İ. M. Abdullayev və b. Bakı-2008.
- Cəbr-həndəsə düsturları, S. X. Rüstəmov, S. S. Rüstəmov, Z. E. Rüstəmova, Xətai kursları, Bakı-2011.


































